工作原理
基本概念
在开发Nodejs应用时,当需要在数据库中存储树时,常见的存储结构有以下几种:
- 邻接列表结构
- 路径枚举结构
- 嵌套树结构
- 闭包表结构
以上算法各有优缺点,应该根据实际的应用场景选择合适的算法。
嵌套树模型(Nested Set Model)也被称为左右值模型,它是一种用于存储树形结构数据的方法,通过两个字段(通常被称为 lft 和 rgt)来表示节点在树中的位置。
在嵌套树模型中,每个节点的lft值都小于其所有子节点的lft值,rgt值都大于其所有子节点的 rgt 值。这样,我们可以通过一个简单的查询来获取一个节点的所有后代,只需要查找lft 和 rgt 值在这个范围内的所有节点即可。
嵌套树模型的左右值分布方式是通过深度优先遍历(Depth-First Search)来确定的。在遍历过程中,每当进入一个节点时,就分配一个 lft 值,每当离开一个节点时,就分配一个 rgt 值。这样,每个节点的 lft 和 rgt 值就形成了一个区间,这个区间内的所有值都对应该节点的子节点。
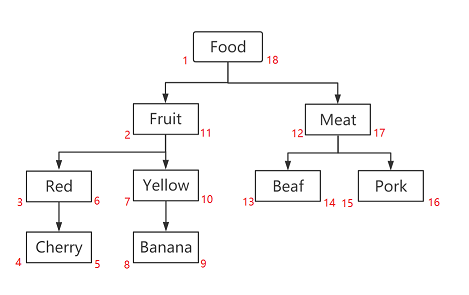
例如,下面是一个嵌套树模型的例子:
| id | leftValue | rightValue | name |
|---|---|---|---|
| 1 | 1 | 14 | root |
| 2 | 2 | 9 | A |
| 3 | 10 | 11 | B |
| 4 | 12 | 13 | C |
| 5 | 3 | 4 | A-1 |
| 6 | 5 | 6 | A-2 |
| 7 | 7 | 8 | A-3 |
这个表表示了如下的树形结构:
- root
- A
- A-1
- A-2
- A-3
- B
- C
- A
扩展
FlexTree就是基于左右值算法的树存储管理组件,采用Typescript开发,适用于任意数据库场景,封装了各种易用的API。
FlexTree在左右值算法的基础上,增加了level字段,用于表示节点的层级。通过level字段,我们可以更方便的获取树的层级结构。如下:
| id | level | leftValue | rightValue | name |
|---|---|---|---|---|
| 1 | 0 | 1 | 14 | root |
| 2 | 1 | 2 | 9 | A |
| 3 | 1 | 10 | 11 | B |
| 4 | 1 | 12 | 13 | C |
| 5 | 2 | 3 | 4 | A-1 |
| 6 | 2 | 5 | 6 | A-2 |
| 7 | 2 | 7 | 8 | A-3 |
方案对比
在数据库中存储树形结构数据时,比较常见用的方案是几种:
- 邻接列表结构
- 路径枚举结构
- 闭包表结构
- 嵌套树结构
与邻接列表结构对比
邻接列表结构每个节点都有一个指向其父节点(pid)的引用。如下:
| id | pid | name |
|---|---|---|
| 1 | NULL | root |
| 2 | 1 | A |
| 3 | 1 | B |
| 4 | 1 | C |
| 5 | 2 | A-1 |
| 6 | 2 | A-2 |
| 7 | 2 | A-3 |
这种方法简单直观,也是最容易理解和常用的方法,但是在查询时需要递归查询,性能较差。
比如我们要实现以下方法:
- 查询某个节点的所有后代节点
- 查询某个节点的所有祖先节点
- 移动某个子树到另一个节点下
- 删除某个节点及其后代子树
这些操作均无法通过简单的1-N条SQL语句实现,需要应用层进行递归查询,树的层级越多,性能较差。
与路径枚举结构对比
正因为邻接列表结构的递归性能问题,所以有了路径枚举结构。路径枚举结构是在邻接列表结构的基础上,增加了一个path字段,用于存储节点的路径。如下:
| id | path | name |
|---|---|---|
| 1 | /root | root |
| 2 | /root/A | A |
| 3 | /root/B | B |
| 4 | /root/C | C |
| 5 | /root/A/A-1 | A-1 |
| 6 | /root/A/A-2 | A-2 |
| 7 | /root/A/A-3 | A-3 |
此种方案的优点是:查询某个节点的所有后代节点时,只需要查询path字段即可,不需要递归查询。但是,当树的层级较多时,但是也存在缺点。
- 查询操作主要是对
path字符串的like操作,性能较差 - 路径可能变得很长,树的层级受限,普通的
VARCHAR可能不够,需要使用TEXT。 - 选择哪个字段拼接
path是个问题.- 如果选择
name作为path字段,当name字段值存在重名、特殊字符、变更时,会导致path字段不唯一或异常。因此作为path字段的字段应该尽量是是唯一的、简短的、变化很少的,且不包含特殊字符。 - 如果选择
id(pk)组合path字段,由于pk具有唯一性并且比较稳定,所以是比较适合作为path字段的。但是如果id字段是uuid类型,那么就导致path字段变得很长,查询效率也相应变低。
- 如果选择
- 移动某个子树到另一个节点下,也相对简单。如将/root/A/A-2移动为/root/B的子节点,执行如下
SQL即可。
UPDATE tree_table
SET path = REPLACE(path, '/root/A/A-2', '/root/B/A-2')
WHERE path LIKE '/root/A/A-2%';- 路径枚举结构的树表是无序树,为了支持有序树,需要额外的字段
order来维护节点的顺序,如下:
| id | path | order | name |
|---|---|---|---|
| 1 | /root | 1 | root |
| 2 | /root/A | 2 | A |
| 3 | /root/A/A-1 | 3 | A-1 |
| 4 | /root/A/A-2 | 4 | A-2 |
| 5 | /root/A/A-3 | 5 | A-3 |
| 6 | /root/B | 6 | B |
| 7 | /root/C | 7 | C |
新引入order将树变成有序树后,维护order字段的逻辑会变得复杂。
总之,我们需要在path字段的选择上做出权衡,以及对path字段的长度和查询效率做出考虑。如果组合成path的字段(如名称)上可能存在重名、特殊字符、变更等情况,则不适合作为path字段。
与闭包表结构对比
闭包表结构需要两张表来表示树,一张表存储节点信息,另一张表存储节点之间的关系。如下:
- 节点表
| id | name |
|---|---|
| 1 | root |
| 2 | A |
| 3 | B |
| 4 | C |
| 5 | A-1 |
| 6 | A-2 |
| 7 | A-3 |
- 关系表
| ancestor | descendant | depth |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 2 |
| 1 | 6 | 2 |
| 1 | 7 | 2 |
| 2 | 2 | 0 |
| 2 | 5 | 1 |
| 2 | 6 | 1 |
| 2 | 7 | 1 |
| 3 | 3 | 0 |
| 4 | 4 | 0 |
| 5 | 5 | 0 |
| 6 | 6 | 0 |
| 7 | 7 | 0 |
- 从上表可以看出,为了查询某个节点的所有后代节点 每个节点需要记录其所有祖先节点,以及每个节点的深度。这样就需要更多的存储空间,且维护成本较高。